Logistic Regression

Thursday. December 21, 2017

preface Logistic regression 은 종속변수가 0/1 로 구성된 binary outcome 이고 설명변수가 continuous 로 구성되어 있을 때 사용 가능한 분석 방법입니다. 모형 적용에 필요한 가정이 적기 때문에 discriminant analysis 보다 널리 사용됩니다.

다음 자료를 참고하였습니다:

• https://stats.stackexchange.com/questions/120329/what-is-the-difference-between-logistic-and-logit-regression

• https://en.wikipedia.org/wiki/Logistic_regression
• https://www.statmethods.net/advstats/glm.html

Logistic, Logit, odds, odds ratio

$\text{logit function}$ :
.
$\text{logit} \left( x \right) = \log \left( \frac{x}{1-x} \right)$

.

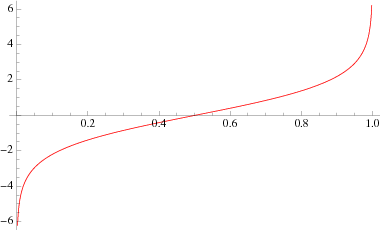
$\text{logistic function}$ :
.
$\text{logistic} \left( x \right) = \frac{ e^{x} }{ 1+e^{x} } = \frac{1}{1+e^{-x}}$

.
$\pi = F\left(X\right) = P \left( Y_i = 1 | X \right)$ : the probability of the event given $X$

$$\begin{aligned} F \left( X \right) &= \text{logistic} \left( X \beta \right) \\ &= \frac{1}{1+e^{- X \beta }} \\ F\left(X\right) \left( 1+e^{- X \beta } \right) &= 1\\ F\left(X\right) + F\left(X\right) e^{- X \beta } &= 1 \\ e^{- X \beta } &= \frac{1-F\left(X\right)}{F\left(X\right)}\\ e^{ X \beta } &= \frac{F\left(X\right)}{1-F\left(X\right)}\\ X \beta &= \log \left( \frac{F\left(X\right)}{1-F\left(X\right)} \right) \\ &= \text{logit} \left( \pi \right) \end{aligned}$$

$F \left( X \right) = \text{logistic} \left( X \beta \right)$
$\phantom{00} = \frac{1}{1+e^{- X \beta }}$

$$\begin{aligned} AR(p): Y_i &= c + \epsilon_i + \phi_i Y_{i-1} \dots \\ Y_{i} &= c + \phi_i Y_{i-1} \dots \end{aligned}$$

$\text{odds}$ : the probability of the event divided by the probability of the event not occurring.

$$\begin{eqnarray*} \text{odds} & = & \frac{\pi}{1-\pi} \\ & = & \exp \left( \text{logit} \left( \pi \right) \right) \\ & = & \frac{\text{logistic} \left( x \right) }{1-\text{logistic} \left( x \right) } \\ &=& \exp \left( X \beta \right) \\ &=& e^{\beta_0 + \beta_1 x_1} \end{eqnarray*}$$

$\text{odds ratio}$ :

$$\begin{eqnarray*} \text{odds ratio} &=& \frac{ \text{odds} \left( x+1 \right) }{\text{odds} \left(x\right) } \\ &=& \frac{e^{\beta_0 + \beta_1 \left(x_1+1\right)}}{e^{\beta_0 + \beta_1 x_1}} \\ &=& e^{\beta_1} \end{eqnarray*}$$

Model Fitting

$$\begin{align} \text{Pr} \left( Y_i = y_i | X_i \right) &=& p_i^{y_i} \left( 1-p_i \right)^{1-y_i} \\ &=& \left( \frac{1}{1+e^{-X\beta}} \right)^{y_i} \left( 1- \frac{1}{1+e^{-X\beta}} \right)^{1-y_i} \end{align}$$ $$\begin{eqnarray*} \text{Pr} \left( Y_i = y_i | X_i \right) &=& p_i^{y_i} \left( 1-p_i \right)^{1-y_i} \\ &=& \left( \frac{1}{1+e^{-X\beta}} \right)^{y_i} \left( 1- \frac{1}{1+e^{-X\beta}} \right)^{1-y_i} \end{eqnarray*}$$ $$\begin{eqnarray*} L \left( \beta | x \right) &=& Pr \left( Y | X ; \beta \right) \\ &=& \prod_i Pr \left( y_i | x_i ; \beta \right) \\ &=& \prod_i \left( \frac{1}{1+e^{-X\beta}} \right)^{y_i} \left( 1- \frac{1}{1+e^{-X\beta}} \right)^{1-y_i} \end{eqnarray*}$$

Log Likelihood

$$\begin{eqnarray*} \frac{1}{N} \text{log} \left( L \left( \beta | x \right) \right) &=& \frac{1}{N} \text{log} \left( \prod_i Pr \left( y_i | x_i ; \beta \right) \right) \\ &=& \frac{1}{N} \sum_i \text{log} \left( Pr \left( y_i | x_i ; \beta \right) \right) \\ &=& \frac{1}{N} \sum_i \text{log} \left( \left( \frac{1}{1+e^{-X\beta}} \right)^{y_i} \left( 1- \frac{1}{1+e^{-X\beta}} \right)^{1-y_i} \right) \\ &=& \frac{1}{N} \sum_i \left( y_i \text{log} \left( \frac{1}{1+e^{-X\beta}} \right) + \left( 1-y_i \right) \text{log} \left( 1- \frac{1}{1+e^{-X\beta}} \right) \right) \end{eqnarray*}$$

.

Logistic Regression in R using glm()

anova(fit1,fit2, test="Chisq") 함수를 사용하여 nested model 비교를 할 수 있습니다. cdplot(F~x, data=mydata) 함수를 사용하면 conditional density plot 을 그릴 수 있습니다.

Tag Cloud

R    SQL    classification    demension reduction    jekyll    python    regression    supervised   

Hyeongjun Kim

Financial Economist, Data Scientist, and Hearthstone Player

Tweet Share